こんにちは。わたくし編集第1グループのK松と申します。編集7年目、医療系雑誌の編集などを経て、現在は教育情報誌を制作しています。
今日は、「植木算」「つるかめ算」といった、小学校『算数』の文章題(主に中学受験の)に用いられる『解法』の話をします。中学校の『数学』以降とは違って、方程式を使わずに解くこれらの手法は一見して迂遠なように見えますが、なかなかどーして算数・数学的な面白さヒラメキが詰まっています。知ってる人は「あー、あったあった、こんな問題解いたよ」と懐かしんでいただき、知らない人は「ふーん、ちょっとした頭の体操になりそう」などと思っていただければうれしいです。(公開:2016年2月22日/更新:2022年4月22日)
食わず嫌いNo.1―算数・数学は、本当は結構面白い!?
算数・数学というと、皆さまはどのようなイメージを思い浮かべますか? 「どうしても克服できなくて私立文系に行ったなあ」という人もいれば、「論理的に解いて唯一の正解を導き出すのが快感だった」といった人もいるかと思います。かく言う私は、数学科で大学に入ったは良いものの大学数学が異次元すぎて初日の講義で心が折れ、文転して経済学科で卒業したという華々しい挫折体験を持つ者です。
ただ、教育情報誌の制作に携わっていると、望むと望まざるとにかかわらず算数について考える機会があり、かつてきっぱり決別したはずの算数と再び向き合わざるを得なくなって、頭を抱えることもしばしばです。ですが、そうして渋々ながらも仕事だからとあれこれ取り組んでいると、今さらにして「あ、算数ってこういう側面もあったんだ」「へえー、算数のこういう考え方、おもしろいなあ」などと気づくこともあり、さながら勘当されて絶縁状態だった父親とふとしたきっかけで和解して対立関係の雪解けを見るような、そんな境地に至る今日この頃であります。
フリーダムな植木職人が招く悲劇、「植木算」
前段が長くなりました。早速ですが、次のような問題を考えてみましょう。
問題
A地点から540m離れたB地点まで、同じ間隔で木を植えることにしました。A地点から15m置きに植えたところ、B地点まで植えることができず、最後の木はB地点の90m手前のところ(C地点)に植えました。次の問いに答えなさい。
1.木は何本ありますか?
2.最後の木をちょうどB地点のところに植えるには、何m置きに植えるとよいですか?
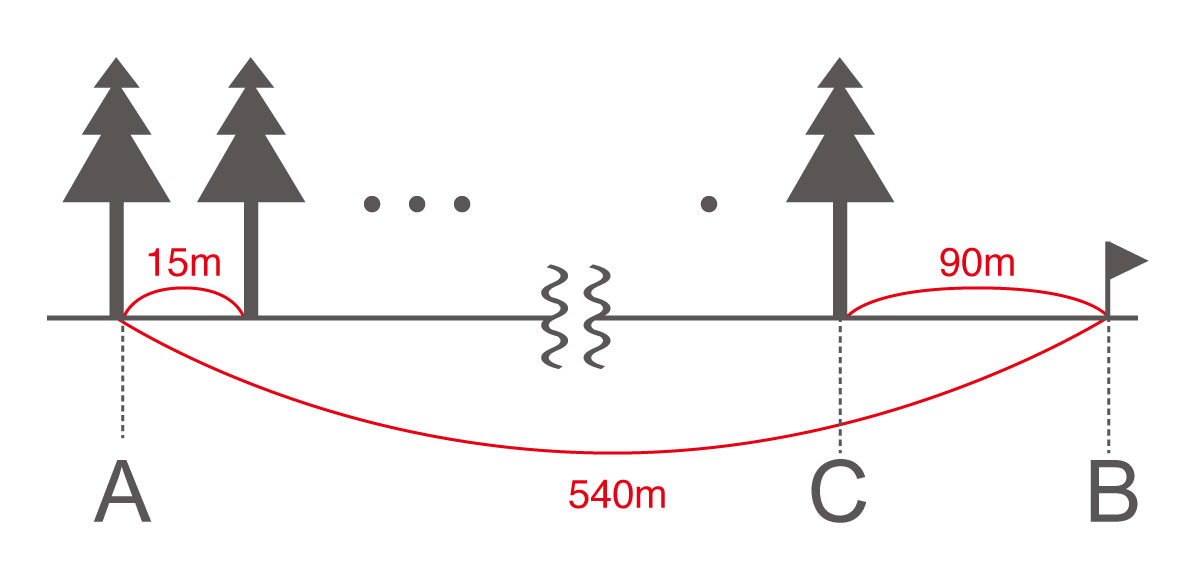
いわゆる“植木算”と呼ばれる文章問題です。この問題の本質は、「物と物のあいだに存在する数に着目する」というところにあります。たとえば、“2本の木”がそれぞれ離れたところに植わっていたとして、その木と木の間に存在するスペースは“1つ”ですね。そんな考え方を念頭に置いて解くと、解答は下記のようになります。
答え
1.
A地点から最後の木が植えてある地点までの距離は、単純計算で下記のように求められます。
540-90=450(m)
そして、木と木のあいだ(スペース)の数は、A地点とC地点の距離(全体の距離)を1か所分のスペースの距離(1単位の距離)で割ることで導き出せます。
450÷15=30(か所)
そして、木の本数と、そのあいだ(スペース)の数の関係性は、こんな式で表せます。
【木の本数】=【そのあいだ(スペース)の数】+1
ゆえに、木の本数は以下のようになります。
30+1=31(本)
2
540m離れたB地点までに31本の木を植えるわけですから、そのあいだ(スペース)の数は、「1.」の計算過程でも出てきたとおり、30か所です。ゆえに、1か所あたりのあいだ(スペース)の長さは、
540÷30=18(m)となります。
いかがでしたでしょうか。解法を見てみると、難しい計算はほとんどしておらず、案外単純なしくみでもって解答を導き出していることがわかります。算数にアレルギーを持っていると、「問題」として出されただけでちょっと身構えてしまう感覚があると思うのですが(少なくとも私はそう)、最初から億劫がらず冷静に向き合えば、意外と何でもないことなのです。
それにしても、この問題の状況設定が現実の出来事だったとしたら大変なことですね。並木道を整備するために等間隔で木を植えなければならない、造園業者さんのお仕事を題材にしたものと拝察しますが、最後に90mも隙間を空けてしまった造園業者さん、うっかりにもほどがあります。責任問題に発展しかねないポカミスですから、この噂は関連業界に瞬く間に広がって、造園業者さんは二度と新しい仕事を受注できなくなってしまうかもしれません。そうならないためにも(?)、この植木算という考え方はとても大切なものだと言えるでしょう。
江戸以前から伝わる歴史的伝統的算数、「つるかめ算」
続いては、つるかめ算です。これは名前を聞いたことがある人も多いのではないでしょうか。
問題
鶴1羽は頭が1つで足が2本、亀1匹は頭が1つで足が4本。ここから、たとえば頭の合計が8つで、足の合計が26本のとき、鶴が何羽で亀が何匹でしょうか?

つるかめ算の考え方をより一般化して言うと、「2種類の量の合計から、それぞれの個数を求める」ってことになります。これは要するに「連立方程式」です。たとえば今のつるかめ算の例で考えると、下記の連立方程式を解くことになります。
答え
鶴の羽数をx、亀の匹数をyと置く。
x+y=8(頭の数から成り立つ式)
2x+4y=26(足の数から成り立つ式)
この式を解くと、x=3、y=5。
すなわち、鶴は3羽、亀は5匹となります。
ただし、この「つるかめ算」はそのほとんどが小学生で登場する問題なのです(現在は、中学受験をする小学生が習う題材として登場するのが一般的)。「連立方程式」という考え方は中学生で習う事柄ですから、小学生はこれを連立方程式ではない方法(xやyなどの代数を使わない方法)を用いて解く必要があります。めんどうくさいですね。ですが、最終的な解答にたどり着くまでに、さまざまな道のり(解法)があるのも、算数・数学の魅力のひとつ。ということで、今度は連立方程式を使わない考え方で解いてみましょう。
答え
まず、足の数の変化に着目してみます。鶴の数が1羽増えると、足の数は2本増えます。鶴と亀の全体の個体数が「8」と固定されている現状を踏まえると、鶴の数が増えるということはすなわち亀の数が1匹減ることになるので、亀の足の数が4本減ることになり、全体の足の数はプラスマイナスで2本減りますね。これが1つ目の前提条件です。
次に、仮に今の全体の個体数「8」が、すべて亀だったと想定すると、4本の足を持つ亀が8匹存在することになるわけですから、4×8=32(本)となり、足の本数の合計は32本となります。これが2つ目の前提条件です。
最後に、設問では「足の合計が26本のとき」の、鶴の羽数と亀の匹数を求めようとしているわけですから、足の本数の誤差は、32-26=6(本)となります。これを1つ目の前提条件に照らし合わせると足6本分、つまり、鶴の羽数にして3羽分の誤差が生じていることがわかります。
これは、全体の個体数「8」がすべて亀だったと想定した場合の話でしたから、よって、実はこのなかの個体には鶴が3羽存在していて、かつその分を差し引きすると亀は当初仮定した8匹ではなく5匹だった、と導きだせます。
(答え)鶴は3羽、亀は5匹
どうでしょう。非常にめんどうくさいですね。私自身、上記の文章を書き起こしていて「めちゃくちゃまどろっこしいことを書いてるな自分」と痛感しました。しばしば、「数学は言語である」と言われるゆえんはこのあたりにあるのではないか、とも思います。なぜって、私がだらだらと日本語で書いてきた鶴と亀にまつわる上記の事柄を、
x+y=8
2x+4y=26
∴x=3、y=5
たったこの3行で表せてしまうのです。はるか古来より、あまたの数学者が、数字と記号の羅列に美的感覚を見いだし、数学的美しさを追求してきた心情の、その一端くらいはわかるような気がします。
歩行力の変わらないただひとつの登場人物たち、「旅人算」
さて、最後は旅人算です。これは、2人が同じ道を歩いている状況で、2人の間の距離を求めたり、2人が向かい合って歩いているときの出会う時間やその速さ、あるいは、2人が同じ方向へ向かって歩いているときの追い越しにかかる時間やその速さ、といった数字を計算するものです。たとえば、「太郎くんが分速70mで家を出発した15分後、お母さんが忘れ物に気づき、自転車で分速250mの速さで追いかけたときの、追いつくまでの時間は?」といった設問が考えられます。この手の問題を目の当たりにすると思わず「太郎くんが忘れ物さえしなければこんな問題は発生しなかったのに……」などと突っ込みを入れたくなるのが人情というもの。しかし、そう侮ってはいけません。実はこの旅人算、私たちの暮らしの非常に身近なところで活用されている考え方なのです。
それは、電車の時刻表(ダイヤグラム)。

(Wikipediaより引用)
電車にはさまざまな種類があるのはご周知のとおり。一つひとつの駅に止まって地元住民の足として活躍している各駅停車のものから、より早く目的地へ到達するためにいくつかの駅を飛ばして走る快速や特急といったもの、そして、大都市間を連結することで旅行やビジネスシーンで重宝する新幹線など、実に多様な電車が世の中には存在します。日本列島を縦横無尽に駆け巡る線路上では、そうしたさまざまな種類の電車を走らせるために、ときに各駅停車の列車がしばし待ち合わせを行って特急列車に追い越させたりするわけですが、そんなときに旅人算の考え方が有効なのです。
では、実際の旅人算の問題を考えてみましょう。
問題
一郎くんが分速65mで出発した10分後に、二郎くんが分速90mで追いかけます。二郎くんが一郎くんに追いつくのは、二郎くんが出発してから何分後でしょうか?
答え
そのほうがわかりやすいかと思いましたので、今回は連立方程式と一次関数を使って解いてみます。まず、設問の状況を一次関数のグラフにすると下記のようになります。
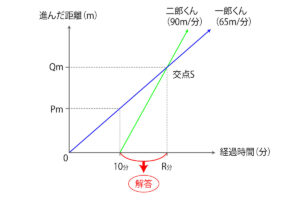
横軸が経過した時間、縦軸が一郎くんと二郎くんの進んだ距離、そして斜めに伸びている2本の線が一郎くんと二郎くんそれぞれの進行過程です。図のなかの交点Sとしている箇所で、二郎くんが一郎くんに追いつくことになります。
一郎くんは分速65mの速さで進んでいるわけですから、横軸の経過時間が1分経つごとに、縦軸で65m進んだことになります。これは、いわゆる「傾き65、切片0」の状態です。だから、一郎くんの進行過程を一次関数の式で表すと、y=65x+0となるわけです(傾き、切片、懐かしいですね。中学校の数学の記憶が蘇ります)。
一方、二郎くんの進行過程を一次関数の式で表すとどうなるのでしょうか。二郎くんの速さは分速90m。ですから、一郎くんのときと同様に、傾きは90とわかります。しかし、二郎くんは10分遅れでスタートしていますから、切片となる場所が一郎くんとは異なります。とりあえず仮に、y=90x+bとしておきましょう。
とはいえ、この切片bはすぐに求めることが可能です。二郎くんは、経過時間10分(x=10)の時点で、まだ一歩も進んでいません(y=0)。なので、これらxとyの数値をそれぞれ式に代入すると、0=90×10+b すなわち b=-900 と求められます。よって、二郎くんの進行過程を一次関数の式で表すと、y=90x-900となるわけです。
さて、いま立てた2つの式、y=65xとy=90x-900、この連立方程式を解いたときに導き出されるxとyの数値が、交点Sの座標です。つるかめ算のときと同じように計算すると、答えはx=36、y=2340。図のなかのアルファベットで表記し直すと、R=36(分)、Q=2340(m)となります。要するに、設問の状況下において、二郎くんが一郎くんに追いつくのは、一郎くんが出発してから36分後、2340m進んだ地点、ということになりますね。
ただし、問題文では「二郎くんが出発してから」とあります。ですから、36-10=26(分)と解答しなくてはならないことに注意が必要です。
(答え)26分後
いかがでしょうか。いま考えた問題は、一郎くんと二郎くんの2人しか登場しませんでしたが、これを電車の時刻表に置き換えてみるとどうなるのでしょう。
一説によると、一日に列車が発着する数が日本で一番多い駅は東京駅だそうですが、その数はおよそ一日4100本。つまり、一日に4100人の一郎くんが東京駅に到着しては発車するような状況だと考えられます。しかもこの一郎くん、車種に応じてそれぞれが違った速度で進みます。そんな一郎くんたち(?)が混乱することなく事故を起こすこともなく、規則正しく整然と時間通りに行き来するという現象は、もはや奇跡といっても過言ではありません。
私は鉄道に関して明るいわけではありませんが、以前、三戸祐子著『定刻発車―日本の鉄道はなぜ世界で最も正確なのか? (新潮文庫)』という本を興味深く読み、そのすごさに触れました。特に、スジ屋と呼ばれるダイヤグラムを作成する人たちの、苦心惨憺の様子には胸が熱くなること請け合いです。上述した一次関数のグラフでいうと、一郎くんや二郎くんの進行過程を表す斜めの線、あの線(スジ)を支障きたすことなく何本も何十本も何百本も、一日の時刻表を作成するために、一枚の紙に書き込んでいくわけですが、そこには、スジ屋の人のみならず鉄道にかかわるすべての人々の涙ぐましい努力が垣間見えます。
算数・数学の力が、そうした場面で大いに有効活用され、私たちの生活を陰ながら支えているのです。
数学がわかると知的でカッコいい――そんな動機で全然OK! 数学に触れてみよう。
今回は、「植木算」「つるかめ算」「旅人算」という3つのテーマについて考えてみました。ここで扱った問題自体はどれも小学生が挑戦するレベルのものでしたが、なかなかどうして、突き詰めて考えていくと「なるほど」と思わされることが多かったのではないかと思います。
ほかにも、「○○算」というテーマは多種多様にあります。方陣算、時計算、流水算、仕事算などなど、身近な題材をもとにしながら算数の本質に迫る考え方は、抽象化・一般化していないからこそストンと腑に落ちるおもしろさがあり、さながら魅力的な謎解きゲームのようです。
昨今は、数学がテーマの中核をなす作品も発表されるようになりました。小川洋子著『博士の愛した数式』や、洋画『ビューティフル・マインド』などは数学者の人生にまつわる物語でした。また、第7回本屋大賞を受賞した冲方丁著『天地明察』では、主人公・渋川春海の、囲碁に秀で、算術を学び、多くの人々の支えのなかで、江戸時代の天文暦学研究において多大な功績を残す、その足跡が描かれています。
* * *
私たちがふだん日常生活を営むうえではあまり意識することのない算数・数学。ですが、算数・数学は、私たちのふだんの日常生活に深く浸透し、その公明正大な論理性は今も力強く息づいているのです。ふと時間を持て余した際には、そんな算数・数学の奥深さに触れてみてはいかがでしょうか。
(図・編集=大山勇一)



